These dice are driving me crazy!

I played a game of Settlers of Catan recently, and was frustrated by the dice rolling.  I'm sure everybody has had this experience, when it seems like statistics have gone out the window.  You start to think that you should have built on that spot with an 11 instead of the spot with the 6, because that what keeps coming up.  It turns out that this is exactly what statistics says should happen, people just aren't very good at thinking about randomness.



I'll start with a quick explanation of how Settlers works.  Each turn you roll two dice with six sides (2d6), then everybody gets resources if their settlements or cities border land that has that number on it.  There are number tiles from 2-12, with little dots on them that tell you how often that number should happen.  So 2 has a single dot, and 6 has five dots.  A good settlement might a 6, a 5 and a 4 for a total of 12 dots.

We're going to take a look at what statistics says should happen in games like this.  First lets just look at rolling 2d6.  The fundamental idea behind trying to figure out what should happen, is that every time you roll a dice, each number on that dice is equally likely.  It will help to understand if the dice are different colors, orange and black. Every time I roll, the orange die will randomly pick a number from 1-6 and the black dice will independently pick a random number from 1-6.  Every number is equally likely for any given die, but if you are interested in the total of both die, then some numbers are more likely than others.

All the possible combinations from rolling two six sided dice.  The black die will randomly select a column, and the orange die will randomly select a row, so you can see that each entry in the table is equally likely.  

The table shows the results from two dice, black and orange, and their sums.  Imagine rolling the black die to pick a column, then rolling the orange die to pick a number from that column, and you will see that each entry in the table is equally likely.  So the probability of getting a certain value in a 2d6 roll is the number of times that value show up in the table, divided by how many numbers are in the table (36).  We can see that 2 should happen 1 time in 36 rolls, and 7 should happen 6 in 36 rolls.  The dots on the number tiles in Settlers of Catan are exactly how many time that number shows up in this table.  So 2 has only one dot, while 6 and 8 have 5 dots.  So if you add up all the dots next to your settlement, you should get one resource per 36/(number of dots) turns.

Probabilities like this don't tell you exactly what is going to happen, they can only tell you about how likely it is that things will happen.  If you roll these dice 6000 times, you will get seven about 1000 times.  But you might get 1032 or 973 or 1001, you can't know in advance.  The typical variation in how many sevens you roll will be roughly the square root of how many you expected to roll based on the probability.  The square root of 1000 is about 30, so you will typically get 1000 sevens to within 30 or so.  If you only roll these dice 36 times, you expect to get 1 two.  The square root of 1 is 1.  This means you expect to have +/- 100% or more variations in how many twos you actually get.   The point is, if you look at a lot of dice rolls, the variations will be a small percent of the total rolls.  But if you look at just a few dice rolls, the variations will be almost as big as the total rolls.  And in board games we almost always look at just a few dice rolls.

I ran some simulations to give you an idea of what this means.  The next two pictures are simulations of rolling 2d6 36 times.  This is like going through 9 turns in a 4 player game of Settlers.  The red lines show how many times each number is expected to come up, and the blue bars show how many times it actually did come up.  You can see that there is huge variation in each set of 9 turns.  In case you haven't seen this type of plot, the x-axis shows the value of the dice rolls, and the y-axis shows how many times it happened.

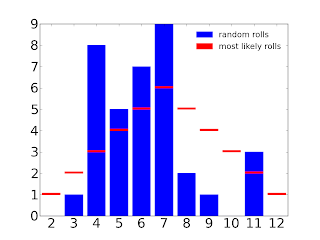Sucks if you have any numbers of 7. 

Looks a bit more like what you expect, but 11s beat 5s and tied 8s.

If you look at a lot more rolls at a time, the results look much more like the expected outcome.  Here is a simulation of 3600 rolls, which is something like 10-20 full games of Settlers.  The variations are a much smaller fraction of the total rolls.

When you look at lots of rolls, the distribution is pretty close to the most likely distribution.

The worst is when you have the resource you need on a good number like an 8, and your opponent crushes you because 11 just keeps coming up.  In small sets of rolls, it is actually pretty common for a crappy number to come up more often than a better number.  Here I ran some simulations to find out how often numbers come up more often than 5.  If you look at sets of 36 rolls, 11 comes up more than 8 over 20% of the time!

What % of the time a number comes up at least as often as 8 in sets of 36 rolls.  If you look at a small number of dice rolls,  any number can come up more often than 8, even 2 or 12.  Its not even very rare.

If instead you look at 3600 rolls, you can basically be guaranteed that the better numbers will come up more often.

What % of the time a number comes up at least as often as 8 in sets of 3600 rolls. Basically, 7 always come up more often than 8, 6 comes up more often about half the time, and nothing else ever comes up more often.  Just like we expect, but it is only like this if you look at lots of rolls at a time.

So now we can see why the dice drive us crazy so often.  If you look at small sets of rolls, statistics say that weird stuff will happen.  Uncommon rolls will come up more often than common rolls, regularly.  It would actually be weird if that didn't happen!  When did the dice screw you over?  Or make the game for you?  Leave a comment.

PS If you want to know more about the statistics of random events, look up the Poisson Distribution.  Can you figure out where I fudged on the math to make the story simpler?